Trong vật lý, hiện tượng giao thoa ánh sáng là một trong những hiện tượng quan trọng và thú vị. Một trong những khái niệm cơ bản liên quan đến hiện tượng này là “khoảng vân”. Bài viết này sẽ giúp bạn hiểu rõ hơn về công thức tính khoảng vân, các yếu tố ảnh hưởng đến khoảng vân, và ứng dụng của nó trong thực tiễn. Đồng thời, chúng tôi cũng sẽ giới thiệu trang web luyenthitienganh.net, một nguồn tài liệu hữu ích cho việc học tập và ôn luyện tiếng Anh.

1. Khái Niệm Về Khoảng Vân
Khoảng vân là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp trên màn giao thoa. Đây là một khái niệm quan trọng trong thí nghiệm giao thoa ánh sáng, đặc biệt là trong thí nghiệm Y-âng. Khoảng vân giúp chúng ta xác định được bước sóng của ánh sáng và các đặc tính của nguồn sáng.
2. Công Thức Tính Khoảng Vân
Công thức tính khoảng vân trong thí nghiệm giao thoa ánh sáng được biểu diễn như sau:
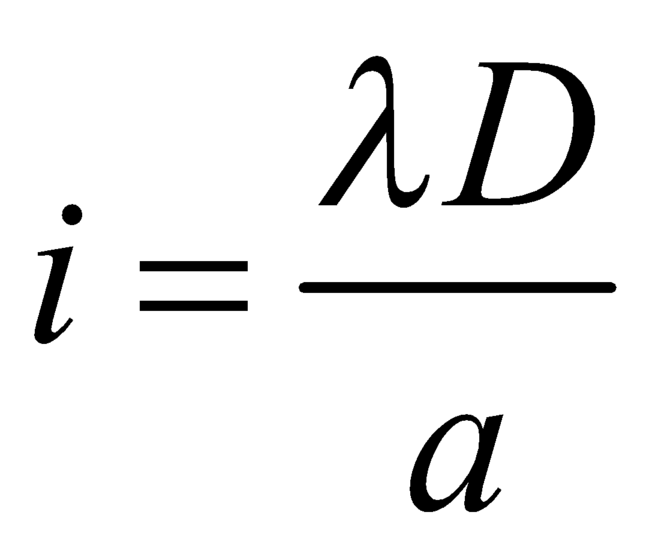
Trong đó:
- i: Khoảng vân (khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp).
- λ: Bước sóng của ánh sáng.
- D: Khoảng cách từ hai khe đến màn.
- a: Khoảng cách giữa hai khe.
Công thức này cho thấy khoảng vân phụ thuộc vào bước sóng của ánh sáng, khoảng cách từ hai khe đến màn, và khoảng cách giữa hai khe.
3. Thí Nghiệm Y-âng Về Giao Thoa Ánh Sáng
Thí nghiệm Y-âng là một trong những thí nghiệm nổi tiếng nhất để chứng minh hiện tượng giao thoa ánh sáng. Trong thí nghiệm này, ánh sáng từ một nguồn sáng đơn sắc được chiếu qua hai khe hẹp song song và sau đó chiếu lên một màn. Trên màn, chúng ta sẽ quan sát được các vân sáng và vân tối xen kẽ nhau, tạo thành một hệ vân giao thoa.
4. Các Yếu Tố Ảnh Hưởng Đến Khoảng Vân
Có một số yếu tố ảnh hưởng đến khoảng vân trong thí nghiệm giao thoa ánh sáng:
- Bước Sóng Ánh Sáng (λ): Bước sóng càng lớn thì khoảng vân càng lớn. Điều này có nghĩa là ánh sáng màu đỏ (bước sóng dài) sẽ tạo ra khoảng vân lớn hơn so với ánh sáng màu xanh (bước sóng ngắn).
- Khoảng Cách Từ Hai Khe Đến Màn (D): Khoảng cách này càng lớn thì khoảng vân càng lớn. Điều này là do ánh sáng có nhiều không gian hơn để giao thoa.
- Khoảng Cách Giữa Hai Khe (a): Khoảng cách này càng nhỏ thì khoảng vân càng lớn. Điều này là do các sóng ánh sáng từ hai khe sẽ giao thoa mạnh mẽ hơn khi chúng gần nhau.
5. Ứng Dụng Của Công Thức Tính Khoảng Vân
Công thức tính khoảng vân có nhiều ứng dụng trong thực tiễn, đặc biệt là trong các lĩnh vực khoa học và kỹ thuật:
- Đo Bước Sóng Ánh Sáng: Bằng cách sử dụng công thức tính khoảng vân, chúng ta có thể xác định được bước sóng của ánh sáng. Điều này rất hữu ích trong các thí nghiệm vật lý và hóa học.
- Kiểm Tra Chất Lượng Quang Học: Công thức này cũng được sử dụng để kiểm tra chất lượng của các thiết bị quang học như kính hiển vi và kính thiên văn.
- Nghiên Cứu Vật Liệu: Trong nghiên cứu vật liệu, công thức tính khoảng vân giúp xác định các đặc tính quang học của vật liệu, chẳng hạn như chiết suất và độ dày của màng mỏng.
6. Ví Dụ Về Tính Khoảng Vân
Để hiểu rõ hơn về cách tính khoảng vân, hãy xem xét một ví dụ cụ thể:
Giả sử chúng ta có một thí nghiệm giao thoa ánh sáng với các thông số sau:
- Bước sóng ánh sáng (λ): 600 nm (nanomet).
- Khoảng cách từ hai khe đến màn (D): 2 m (met).
- Khoảng cách giữa hai khe (a): 0.5 mm (milimet).
Áp dụng công thức tính khoảng vân:
i=aλD=0.5×10−3600×10−9×2=2.4×10−3 m=2.4 mm
Vậy, khoảng vân trong thí nghiệm này là 2.4 mm.
7. Luyện Thi Tiếng Anh Với luyenthitienganh.net
Trang web luyenthitienganh.net là một nguồn tài liệu hữu ích cho việc học tập và ôn luyện tiếng Anh. Tại đây, bạn có thể tìm thấy nhiều bài học, bài tập và tài liệu ôn thi giúp nâng cao kỹ năng tiếng Anh của mình. Đặc biệt, trang web cung cấp các bài học liên quan đến từ vựng và ngữ pháp chuyên ngành, giúp bạn hiểu rõ hơn về các khái niệm khoa học và kỹ thuật bằng tiếng Anh.
8. Kết Luận
Công thức tính khoảng vân là một công cụ quan trọng trong thí nghiệm giao thoa ánh sáng, giúp chúng ta hiểu rõ hơn về các đặc tính của ánh sáng và các yếu tố ảnh hưởng đến hiện tượng giao thoa. Việc nắm vững công thức này không chỉ giúp bạn trong các môn học vật lý mà còn mở rộng hiểu biết về các ứng dụng thực tiễn trong cuộc sống. Để hiểu rõ hơn về các khái niệm và ứng dụng của công thức tính khoảng vân, bạn có thể tham khảo thêm các tài liệu học tập và ôn luyện tại luyenthitienganh.net.
Hy vọng bài viết này đã cung cấp cho bạn những thông tin cần thiết về công thức tính khoảng vân và các ứng dụng của nó. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với chúng tôi qua luyenthitienganh.net để được hỗ trợ thêm. Chúc bạn học tập tốt và thành công trong các kỳ thi sắp tới!
